CF116A.Tram

普及/提高-

通过率：0%

AC君温馨提醒

该题目为【codeforces】题库的题目，您提交的代码将被提交至codeforces进行远程评测，并由ACGO抓取测评结果后进行展示。由于远程测评的测评机由其他平台提供，我们无法保证该服务的稳定性，若提交后无反应，请等待一段时间后再进行重试。

题目描述

Linear Kingdom has exactly one tram line. It has $n$ stops, numbered from $1$ to $n$ in the order of tram's movement. At the $i$ -th stop $a_{i}$ passengers exit the tram, while $b_{i}$ passengers enter it. The tram is empty before it arrives at the first stop. Also, when the tram arrives at the last stop, all passengers exit so that it becomes empty.

Your task is to calculate the tram's minimum capacity such that the number of people inside the tram at any time never exceeds this capacity. Note that at each stop all exiting passengers exit before any entering passenger enters the tram.

输入格式

The first line contains a single number $n$ ( $2<=n<=1000$ ) — the number of the tram's stops.

Then $n$ lines follow, each contains two integers $a_{i}$ and $b_{i}$ ( $0<=a_{i},b_{i}<=1000$ ) — the number of passengers that exits the tram at the $i$ -th stop, and the number of passengers that enter the tram at the $i$ -th stop. The stops are given from the first to the last stop in the order of tram's movement.

The number of people who exit at a given stop does not exceed the total number of people in the tram immediately before it arrives at the stop. More formally, 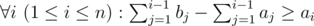. This particularly means that $a_{1}=0$ .
At the last stop, all the passengers exit the tram and it becomes empty. More formally, .
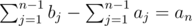No passenger will enter the train at the last stop. That is, $b_{n}=0$ .

输出格式

Print a single integer denoting the minimum possible capacity of the tram (0 is allowed).

输入输出样例

输入#1
```
4
0 3
2 5
4 2
4 0
```
输出#1
```
6
```

说明/提示

For the first example, a capacity of 6 is sufficient:

At the first stop, the number of passengers inside the tram before arriving is 0. Then, 3 passengers enter the tram, and the number of passengers inside the tram becomes 3.
At the second stop, 2 passengers exit the tram (1 passenger remains inside). Then, 5 passengers enter the tram. There are 6 passengers inside the tram now.
At the third stop, 4 passengers exit the tram (2 passengers remain inside). Then, 2 passengers enter the tram. There are 4 passengers inside the tram now.
Finally, all the remaining passengers inside the tram exit the tram at the last stop. There are no passenger inside the tram now, which is in line with the constraints.

Since the number of passengers inside the tram never exceeds 6, a capacity of 6 is sufficient. Furthermore it is not possible for the tram to have a capacity less than 6. Hence, 6 is the correct answer.

首页