CF68A.Irrational problem

Little Petya was given this problem for homework:

You are given function 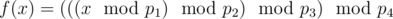(here 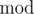represents the operation of taking the remainder). His task is to count the number of integers x in range [a;b] with property f(x) = x.

It is a pity that Petya forgot the order in which the remainders should be taken and wrote down only 4 numbers. Each of 24 possible orders of taking the remainder has equal probability of being chosen. For example, if Petya has numbers 1, 2, 3, 4 then he can take remainders in that order or first take remainder modulo 4, then modulo 2, 3, 1. There also are 22 other permutations of these numbers that represent orders in which remainder can be taken. In this problem 4 numbers wrote down by Petya will be pairwise distinct.

Now it is impossible for Petya to complete the task given by teacher but just for fun he decided to find the number of integers 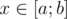with property that probability that f(x) = x is not less than 31.4159265352718281828459045%. In other words, Petya will pick up the number x if there exist at least 7 permutations of numbers _p_1, _p_2, _p_3, _p_4, for which f(x) = x.

小佩特亚的家庭作业中有这样一道题：

给定函数 （其中 表示取模运算）。他的任务是统计区间 [a, b] 中满足 f(x) = x 的整数 x 的个数。

遗憾的是，佩特亚忘记了取模运算的顺序，仅记录下了 4 个数字。所有 24 种可能的取模顺序（即这 4 个数字的全部排列）被选中的概率均等。例如，若佩特亚记下的数字为 1、2、3、4，则他可能按此顺序取模，也可能先对 4 取模、再对 2 取模、接着对 3 取模、最后对 1 取模；此外还有其余 22 种该四元组的排列，每一种都对应一种可能的取模顺序。本题中佩特亚所记录的 4 个数字两两互异。

如今佩特亚已无法完成老师布置的原题，但出于兴趣，他决定找出满足如下条件的整数 的个数：使得 f(x) = x 成立的概率不小于 31.4159265352718281828459045%。换言之，佩特亚将选取整数 x，当且仅当在 _p_₁, _p_₂, _p_₃, _p_₄ 的所有排列中，至少有 7 种排列使得 f(x) = x 成立。

First line of the input will contain 6 integers, separated by spaces: _p_1, _p_2, _p_3, _p_4, a, b (1 ≤ _p_1, _p_2, _p_3, _p_4 ≤ 1000, 0 ≤ a ≤ b ≤ 31415).

It is guaranteed that numbers _p_1, _p_2, _p_3, _p_4 will be pairwise distinct.

输入的第一行包含 6 个整数，以空格分隔：$p_1,\,p_2,\,p_3,\,p_4,\,a,\,b$（其中 $1 \le p_1,\,p_2,\,p_3,\,p_4 \le 1000$，$0 \le a \le b \le 31415$）。

保证 $p_1,\,p_2,\,p_3,\,p_4$ 两两互不相同。

Output the number of integers in the given range that have the given property.

输出给定范围内满足给定性质的整数个数。